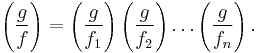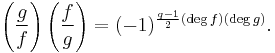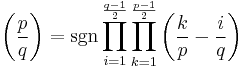Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers. There are a number of equivalent statements of the theorem, which consists of two "supplements" and the reciprocity law:
Let p, q > 2 be two distinct (positive odd) prime numbers. Then
(Supplement 1)
- x2 ≡ −1 (mod p) is solvable if and only if p ≡ 1 (mod 4).
(Supplement 2)
- x2 ≡ 2 (mod p) is solvable if and only if p ≡ ±1 (mod 8).
(Quadratic reciprocity)
Let q * = ±q where the sign is plus if q ≡ 1 (mod 4) and minus if q ≡ −1 (mod 4). (I.e. |q *| = q and q * ≡ 1 (mod 4).) Then
- x2 ≡ p (mod q) is solvable if and only if x2 ≡ q * (mod p) is solvable.
Although the law can be used to tell whether any quadratic equation modulo a prime number has a solution, it does not provide any help at all for actually finding the solution. (The article on quadratic residues discusses algorithms for this.)
The theorem was conjectured by Euler and Legendre and first proven by Gauss.[1] He refers to it as the "fundamental theorem" in the Disquisitiones Arithmeticae and his papers; privately he referred to it as the "golden theorem."[2] He published six proofs, and two more were found in his posthumous papers. There are now over 200 published proofs.[3]
The first section of this article does not use the Legendre symbol and gives the formulations of quadratic reciprocity found by Legendre and Gauss. The Legendre-Jacobi symbol is introduced in the second section.
Contents |
Terminology, data, and two statements of the theorem
A quadratic residue (mod n) is any number congruent to a square (mod n). A quadratic nonresidue (mod n) is any number which is not congruent to a square (mod n). The adjective "quadratic" can be dropped if the context makes it clear that it is implied. When working modulo primes (as in this article), it is usual to treat zero as a special case. By doing so, the following statements become true:
Modulo a prime, there are an equal number of quadratic residues and nonresidues.
Modulo a prime, the product of two quadratic residues is a residue, the product of a residue and a nonresidue is a nonresidue, and the product of two nonresidues is a residue.
Table of quadratic residues
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 |
| mod 3 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| mod 5 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 | 1 | 4 | 4 | 1 | 0 |
| mod 7 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 |
| mod 11 | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| mod 13 | 1 | 4 | 9 | 3 | 12 | 10 | 10 | 12 | 3 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 3 | 12 | 10 | 10 | 12 | 3 | 9 | 4 | 1 |
| mod 17 | 1 | 4 | 9 | 16 | 8 | 2 | 15 | 13 | 13 | 15 | 2 | 8 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 8 | 2 | 15 | 13 |
| mod 19 | 1 | 4 | 9 | 16 | 6 | 17 | 11 | 7 | 5 | 5 | 7 | 11 | 17 | 6 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 6 | 17 |
| mod 23 | 1 | 4 | 9 | 16 | 2 | 13 | 3 | 18 | 12 | 8 | 6 | 6 | 8 | 12 | 18 | 3 | 13 | 2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 |
| mod 29 | 1 | 4 | 9 | 16 | 25 | 7 | 20 | 6 | 23 | 13 | 5 | 28 | 24 | 22 | 22 | 24 | 28 | 5 | 13 | 23 | 6 | 20 | 7 | 25 | 16 |
| mod 31 | 1 | 4 | 9 | 16 | 25 | 5 | 18 | 2 | 19 | 7 | 28 | 20 | 14 | 10 | 8 | 8 | 10 | 14 | 20 | 28 | 7 | 19 | 2 | 18 | 5 |
| mod 37 | 1 | 4 | 9 | 16 | 25 | 36 | 12 | 27 | 7 | 26 | 10 | 33 | 21 | 11 | 3 | 34 | 30 | 28 | 28 | 30 | 34 | 3 | 11 | 21 | 33 |
| mod 41 | 1 | 4 | 9 | 16 | 25 | 36 | 8 | 23 | 40 | 18 | 39 | 21 | 5 | 32 | 20 | 10 | 2 | 37 | 33 | 31 | 31 | 33 | 37 | 2 | 10 |
| mod 43 | 1 | 4 | 9 | 16 | 25 | 36 | 6 | 21 | 38 | 14 | 35 | 15 | 40 | 24 | 10 | 41 | 31 | 23 | 17 | 13 | 11 | 11 | 13 | 17 | 23 |
| mod 47 | 1 | 4 | 9 | 16 | 25 | 36 | 2 | 17 | 34 | 6 | 27 | 3 | 28 | 8 | 37 | 21 | 7 | 42 | 32 | 24 | 18 | 14 | 12 | 12 | 14 |
This table is complete for primes less than 50. To check whether a number n is a quadratic residue mod one of these primes p, find a ≡ n (mod p) and 0 ≤ a < p. If a is in row p it is a residue (mod p); if it is not in row p of the table, it is a nonresidue (mod p).
The quadratic reciprocity law is the statement that certain patterns found in the table are true in general.
In this article, p and q always refer to distinct positive odd prime numbers.
–1 and the first supplement
First of all, for which prime numbers is –1 a quadratic residue? Examining the table, we find –1 in rows 5, 13, 17, 29, 37, and 41 but not in rows 3, 7, 11, 19, 23, 31, 43 or 47.
(–1 ≡ 2 (mod 3), –1 ≡ 4 (mod 5), –1 ≡ 10 (mod 11), etc.)
The former primes are all ≡ 1 (mod 4), and the latter are all ≡ 3 (mod 4). This leads to
The first supplement to quadratic reciprocity:
±2 and the second supplement
For which prime numbers is 2 a quadratic residue? Examining the table, we find 2 in rows 7, 17, 23, 31, 41, and 47, but not in rows 3, 5, 11, 13, 19, 29, 37, or 43.
The former primes are all ≡ ±1 (mod 8), and the latter are all ≡ ±3 (mod 8). This leads to
The second supplement to quadratic reciprocity:
–2 is in rows 3, 11, 17, 19, 41, 43, but not in rows 5, 7, 13, 23, 29, 31, 37, or 47. The former are ≡ 1 or ≡ 3 (mod 8), and the latter are ≡ 5 or ≡ 7 (mod 8).
±3
3 is in rows 11, 13, 23, 37, and 47, but not in rows 5, 7, 17, 19, 29, 31, 41, or 43.
The former are ≡ ±1 (mod 12) and the latter are all ≡ ±5 (mod 12).
–3 is in rows 7, 13, 19, 31, 37, and 43 but not in rows 5, 11, 17, 23, 29, 41, or 47. The former are ≡ 1 (mod 3) and the latter ≡ 2 (mod 3).
Since the only residue (mod 3) is 1, we see that –3 is a quadratic residue modulo every prime which is a residue (mod 3).
±5
5 is in rows 11, 19, 29, 31, and 41 but not in rows 3, 7, 13, 17, 23, 37, 43, or 47.
The former are ≡ ±1 (mod 5) and the latter are ≡ ±2 (mod 5).
Since the only residues (mod 5) are ±1, we see that 5 is a quadratic residue modulo every prime which is a residue (mod 5).
–5 is in rows 3, 7, 23, 29, 41, 43, and 47 but not in rows 11, 13, 17, 19, 31, or 37. The former are ≡ 1, 3, 7, 9 (mod 20) and the latter are ≡ 11, 13, 17, 19 (mod 20).
Gauss's version
The observations about –3 and +5 continue to hold: –7 is a residue (mod p) if and only if p is a residue (mod 7), –11 is a residue (mod p) if and only if p is a residue (mod 11), +13 is a residule (mod p) if and only if p is a residue (mod 13), ...
The more complicated-looking rules for the quadratic characters of +3 and –5, which depend upon congruences (mod 12) and (mod 20) respectively, are simply the ones for –3 and +5 working with the first supplement.
For example, for –5 to be a residue (mod p), either both 5 and –1 have to be residues (mod p) or they both have to be nonresidues: i.e., p has to be ≡ ±1 (mod 5) and ≡ 1 (mod 4), which is the same thing as p ≡ 1 or 9 (mod 20), or p has to be ≡ ±2 mod 5 and ≡ 3 mod 4, which is the same as p ≡ 3 or 7 (mod 20). See Chinese remainder theorem.
The generalization of the rules for –3 and +5 is Gauss's statement of quadratic reciprocity:
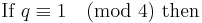
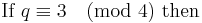
These statements may be combined:
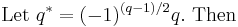
Table of quadratic character of primes
| R | q is a residue (mod p) | q ≡ 1 (mod 4) or p ≡ 1 (mod 4) (or both) |
| N | q is a nonresidue (mod p) | |
| R | q is a residue (mod p) | both q ≡ 3 (mod 4) and p ≡ 3 (mod 4) |
| N | q is a nonresidue (mod p) |
| q | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 | ||
| p | 3 | N | R | N | R | N | R | N | N | R | R | N | R | N | N | N | R | R | N | R | R | N | N | R | |
| 5 | N | N | R | N | N | R | N | R | R | N | R | N | N | N | R | R | N | R | N | R | N | R | N | ||
| 7 | N | N | R | N | N | N | R | R | N | R | N | R | N | R | N | N | R | R | N | R | N | N | N | ||
| 11 | R | R | N | N | N | N | R | N | R | R | N | N | R | R | R | N | R | R | N | N | N | R | R | ||
| 13 | R | N | N | N | R | N | R | R | N | N | N | R | N | R | N | R | N | N | N | R | N | N | N | ||
| 17 | N | N | N | N | R | R | N | N | N | N | N | R | R | R | R | N | R | N | N | N | R | R | N | ||
| 19 | N | R | R | R | N | R | R | N | N | N | N | R | R | N | N | R | N | N | R | N | R | N | N | ||
| 23 | R | N | N | N | R | N | N | R | R | N | R | N | R | N | R | N | N | R | R | N | N | N | N | ||
| 29 | N | R | R | N | R | N | N | R | N | N | N | N | N | R | R | N | R | R | N | N | R | N | N | ||
| 31 | N | R | R | N | N | N | R | N | N | N | R | N | R | N | R | N | R | R | N | N | N | N | R | ||
| 37 | R | N | R | R | N | N | N | N | N | N | R | N | R | R | N | N | R | R | R | N | R | N | N | ||
| 41 | N | R | N | N | N | N | N | R | N | R | R | R | N | N | R | R | N | N | R | N | R | N | N | ||
| 43 | N | N | N | R | R | R | N | R | N | R | N | R | R | R | R | N | R | N | N | R | R | N | R | ||
| 47 | R | N | R | N | N | R | N | N | N | N | R | N | N | R | R | R | N | R | N | R | R | R | R | ||
| 53 | N | N | R | R | R | R | N | N | R | N | R | N | R | R | R | N | N | N | N | N | N | R | R | ||
| 59 | R | R | R | N | N | R | R | N | R | N | N | R | N | N | R | N | N | R | N | R | N | N | N | ||
| 61 | R | R | N | N | R | N | R | N | N | N | N | R | N | R | N | N | N | N | R | N | R | N | R | ||
| 67 | N | N | N | N | N | R | R | R | R | N | R | N | N | R | N | R | N | R | R | N | R | R | N | ||
| 71 | R | R | N | N | N | N | R | N | R | N | R | N | R | N | N | N | N | N | R | R | R | R | N | ||
| 73 | R | N | N | N | N | N | R | R | N | N | R | R | N | N | N | N | R | R | R | R | N | R | R | ||
| 79 | N | R | N | R | R | N | R | R | N | R | N | N | N | N | N | N | N | R | N | R | R | R | R | ||
| 83 | R | N | R | R | N | R | N | R | R | R | R | R | N | N | N | R | R | N | N | N | N | N | N | ||
| 89 | N | R | N | R | N | R | N | N | N | N | N | N | N | R | R | N | N | R | R | R | R | N | R | ||
| 97 | R | N | N | R | N | N | N | N | N | R | N | N | R | R | R | N | R | N | N | R | R | N | R | ||
Legendre's version
Another way to organize the data is to see which primes are residues mod which other primes, as illustrated in the above table. The entry in row p column q is R if q is a quadratic residue (mod p); if it is a nonresidue the entry is N.
If the row, or the column, or both, are ≡ 1 (mod 4) the entry is blue or green; if both row and column are ≡ 3 (mod 4), it is yellow or orange.
The blue and green entries are symmetric around the diagonal: The entry for row p, column q is R (resp N) if and only if the entry at row q, column p, is R (resp N).
The yellow and orange ones, on the other hand, are antisymmetric: The entry for row p, column q is R (resp N) if and only if the entry at row q, column p, is N (resp R).
This observation is Legendre's statement of quadratic reciprocity:
It is a simple exercise to prove that Legendre's and Gauss's statements are equivalent - it requires no more than the first supplement and the facts about multiplying residues and nonresidues.
History and alternative statements
There are a number of ways to state the theorem. Keep in mind that Euler and Legendre did not have Gauss's congruence notation, nor did Gauss have the Legendre symbol.
In this article p and q always refer to distinct positive odd primes.
Fermat
Fermat proved[4] (or claimed to have proved)[5] a number of theorems about expressing a prime by a quadratic form:
He did not state the law of quadratic reciprocity, although the cases −1, ±2, and ±3 are easy deductions from these and other of his theorems.
He also claimed to have a proof that if the prime number p ends with 7, (in base 10) and the prime number q ends in 3, and p ≡ q ≡ 3 (mod 4), then
Euler conjectured, and Lagrange proved, that[6]
Proving these and other statements of Fermat was one of the things that led mathematicians to the reciprocity theorem.
Euler
Translated into modern notation, Euler stated:[7]
1) If q ≡ 1 (mod 4) then q is a quadratic residue (mod p) if and only if p ≡ r (mod q), where r is a quadratic residue of q.
2) If q ≡ 3 (mod 4) then q is a quadratic residue (mod p) if and only if p ≡ ±b2 (mod 4q), where b is odd and not divisible by q.
This is equivalent to quadratic reciprocity.
He could not prove it, but he did prove the second supplement.[8]
Legendre and his symbol
Fermat proved that if p is a prime number and a is an integer,
Thus, if p does not divide a,
Legendre[9] lets a and A represent positive primes ≡ 1 (mod 4) and b and B positive primes ≡ 3 (mod 4), and sets out a table of eight theorems that together are equivalent to quadratic reciprocity:
| Theorem | When | it follows that |
|---|---|---|
| I | 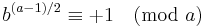 |
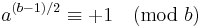 |
| II | 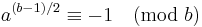 |
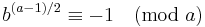 |
| III | 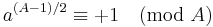 |
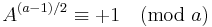 |
| IV | 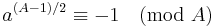 |
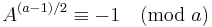 |
| V | 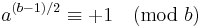 |
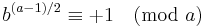 |
| VI | 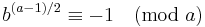 |
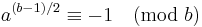 |
| VII | 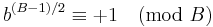 |
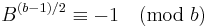 |
| VIII | 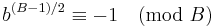 |
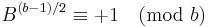 |
He says that since expressions of the form
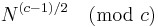 (where N and c are relatively prime) will come up so often he will abbreviate them as:
(where N and c are relatively prime) will come up so often he will abbreviate them as:
This is now known as the Legendre symbol, and an equivalent[10][11] definition is used today: for all integers a and all odd primes p
Legendre's version of quadratic reciprocity
He notes that these can be combined:
A number of proofs, especially those based on Gauss's Lemma,[12] explicitly calculate this formula.
The supplementary laws using Legendre symbols
Legendre's attempt to prove reciprocity is based on a theorem of his:
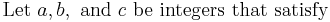
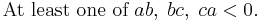 (i.e. they don't all have the same sign)
(i.e. they don't all have the same sign)
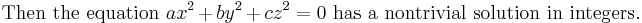
E.g., Theorem I is handled by letting a ≡ 1 and b ≡ 3 (mod 4) be primes and assuming that 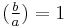 and, contrary the theorem, that
and, contrary the theorem, that 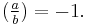 Then
Then 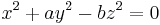 has a solution, and taking congruences (mod 4) leads to a contradiction.
has a solution, and taking congruences (mod 4) leads to a contradiction.
This technique doesn't work for Theorem VIII. Let b ≡ B ≡ 3 (mod 4), and assume 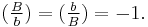 Then if there is another prime p ≡ 1 (mod 4) such that
Then if there is another prime p ≡ 1 (mod 4) such that 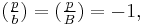 the solvability of
the solvability of 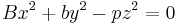 leads to a contradiction (mod 4). But Legendre was unable to prove there has to be such a prime p; he was later able to show that all that is required is "Legendre's lemma":
leads to a contradiction (mod 4). But Legendre was unable to prove there has to be such a prime p; he was later able to show that all that is required is "Legendre's lemma":
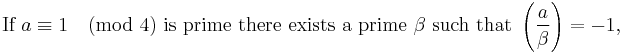
but he couldn't prove that either. Hilbert symbol (below) discusses how techniques based on the existence of solutions to  can be made to work.
can be made to work.
Gauss

Gauss first proves[13] the supplementary laws. He sets[14] the basis for induction by proving the theorem for ±3 and ±5. Noting[15] that it is easier to state for –3 and +5 than it is for +3 or –5, he states[16] the general theorem in the form:
If p is a prime of the form 4n+1 then p, but if p is of the form 4n+3 then –p, is a quadratic residue (resp. nonresidue) of every prime, which, with a positive sign, is a residue (resp. nonresidue) of p.
In the next sentence, he christens it the fundamental theorem (Gauss never used the word "reciprocity").
Introducing the notation a R b (resp. a N b) to mean a is a quadratic residue (resp. nonresidue) (mod b), and letting a, a′, etc. represent positive primes ≡ 1 (mod 4) and b, b′, etc. positive primes ≡ 3 (mod 4), he breaks it out into the same 8 cases as Legendre:
| Case | If | Then |
|---|---|---|
| 1) | ±a R a′ | ±a′ R a |
| 2) | ±a N a′ | ±a′ N a |
| 3) | +a R b –a N b |
±b R a |
| 4) | +a N b –a R b |
±b N a |
| 5) | ±b R a | +a R b –a N b |
| 6) | ±b N a | +a N b –a R b |
| 7) | +b R b′ –b N b′ |
–b′ N b +b′ R b |
| 8) | –b N b′ +b R b′ |
+b′ R b –b′ N b |
In the next Article he generalizes this to what are basically the rules for the Jacobi symbol (below). Letting A, A′, etc. represent any (prime or composite) positive numbers ≡ 1 (mod 4) and B, B′, etc. positive numbers ≡ 3 (mod 4):
| Case | If | Then |
|---|---|---|
| 9) | ±a R A | ±A R a |
| 10) | ±b R A | +A R b –A N b |
| 11) | +a R B | ±B R a |
| 12) | –a R B | ±B N a |
| 13) | +b R B | –B N b +N R b |
| 14) | –b R B | +B R b –B N b |
All of these cases take the form "if a prime is a residue (mod a composite), then the composite is a residue or nonresidue (mod the prime), depending on the congruences (mod 4)". He proves that these follow from cases 1) - 8).
Gauss needed, and was able to prove,[17] a lemma similar to the one Legendre needed: 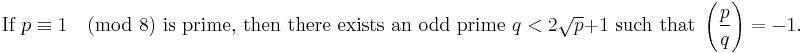
The proof[18] of quadratic reciprocity is by complete induction (i.e. assuming it is true for all numbers less than n allows the deduction it is true for n) for each of the cases 1) to 8).
Gauss's version in Legendre symbols
These can be combined:
A number of proofs of the theorem, especially those based on Gauss sums,[19] or the splitting of primes in algebraic number fields,[20] derive this formula.
Other statements
Note that the statements in this section are equivalent to quadratic reciprocity: if, for example, Euler's version is assumed, the Legendre-Gauss version can be deduced from it, and vice-versa.
Euler
This form of quadratic reciprocity is derived from Euler's work:[21]
Euler's statement can be proved by using Gauss's lemma.
Gauss
Gauss's fourth proof[22] consists of proving this theorem (by comparing two formulas for the value of Gauss sums) and then restricting it to two primes:
Let a, b, c, ... be unequal positive odd primes, whose product is n, and let m be the number of them that are ≡ 3 (mod 4); check whether n/a is a residue of a, whether n/b is a residue of b, .... The number of nonresidues found will be even when m ≡ 0, 1 (mod 4), and it will be odd if m ≡ 2, 3 (mod 4).
He gives the example. Let a = 3, b = 5, c = 7, and d = 11. Three of these, 3, 7, and 11 ≡ 3 (mod 4), so m ≡ 3 (mod 4).
5×7×11 R 3; 3×7×11 R 5; 3×5×11 R 7; and 3×5×7 N 11, so there are an odd number of nonresidues.
Eisenstein
Eisenstein[23] formulates this:
Mordell
Mordell[24] proved that this is equivalent to quadratic reciprocity:
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol; the main difference is that the bottom number has to be positive and odd, but does not have to be prime. If it is prime, the two symbols agree. It obeys the same rules of manipulation as the Legendre symbol. In particular
and if both numbers are positive and odd (this is sometimes called "Jacobi's reciprocity law"):
However, if the Jacobi symbol is +1 and the bottom number is composite, it does not necessarily mean that the top number is a quadratic residue of the bottom one. Gauss's cases 9) - 14) above can be expressed in terms of Jacobi symbols:
and since p is prime the left hand side is a Legendre symbol, and we know whether M is a residue (mod p) or not.
The formulas listed in the preceding section are true for Jacobi symbols as long as the symbols are defined. Euler's formula may be written
For example,
and 2 is a residue mod the primes 7, 23 and 31: 32 ≡ 2 (mod 7), 52 ≡ 2 (mod 23), and 82 ≡ 2 (mod 31), but 2 is not a quadratic residue (mod 5), so it can't be one (mod 15). This is related to the problem Legendre had: if we know that
, we know that a is a nonresidue modulo every prime in the arithmetic series m + 4a, m + 8a, ..., if there are any primes in this series, but that wasn't proved until decades[25] after Legendre.
Eisenstein's formula requires relative primality conditions (which are true if the numbers are prime)
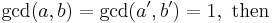
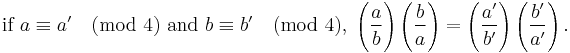
Hilbert symbol
The quadratic reciprocity law can be formulated in terms of the Hilbert symbol 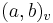 where a and b are any two nonzero rational numbers and v runs over all the non-trivial absolute values of the rationals (the archimedean one and the p-adic absolute values for primes p). The Hilbert symbol
where a and b are any two nonzero rational numbers and v runs over all the non-trivial absolute values of the rationals (the archimedean one and the p-adic absolute values for primes p). The Hilbert symbol 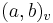 is 1 or −1. It is defined to be 1 if and only if the equation
is 1 or −1. It is defined to be 1 if and only if the equation 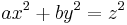 has a solution in the completion of the rationals at v other than
has a solution in the completion of the rationals at v other than  . The Hilbert reciprocity law states that
. The Hilbert reciprocity law states that 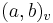 , for fixed a and b and varying v, is 1 for all but finitely many v and the product of
, for fixed a and b and varying v, is 1 for all but finitely many v and the product of 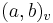 over all v is 1. (This formally resembles the residue theorem from complex analysis.)
over all v is 1. (This formally resembles the residue theorem from complex analysis.)
The proof of Hilbert reciprocity reduces to checking a few special cases, and the non-trivial cases turn out to be equivalent to the main law and the two supplementary laws of quadratic reciprocity for the Legendre symbol. There is no kind of reciprocity in the Hilbert reciprocity law; its name simply indicates the historical source of the result in quadratic reciprocity. Unlike quadratic reciprocity, which requires sign conditions (namely positivity of the primes involved) and a special treatment of the prime 2, the Hilbert reciprocity law treats all absolute values of the rationals on an equal footing. Therefore it is a more natural way of expressing quadratic reciprocity with a view towards generalization: the Hilbert reciprocity law extends with very few changes to all global fields and this extension can rightly be considered a generalization of quadratic reciprocity to all global fields.
Other rings
There are also quadratic reciprocity laws in rings other than the integers.
Gaussian integers
In his second monograph on quartic reciprocity[26] Gauss stated quadratic reciprocity for the ring Z[i] of Gaussian integers, saying that it is a corollary of the biquadratic law in Z[i], but did not provide a proof of either theorem. Dirichlet[27] showed that the law in Z[i] can be deduced from the law for Z without using biquadratic reciprocity.
For an odd Gaussian prime π and a Gaussian integer α, gcd(α, π) = 1, define the quadratic character for Z[i] by the formula
Let λ = a + b i and μ = c + d i be distinct Gaussian primes where a and c are odd and b and d are even. Then[28]
where 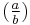 is the Jacobi symbol for Z.
is the Jacobi symbol for Z.
Eisenstein integers
The ring of Eisenstein integers is Z[ω], where 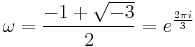 is a cube root of 1. (See the articles on Eisenstein integer and cubic reciprocity for definitions and notations).
is a cube root of 1. (See the articles on Eisenstein integer and cubic reciprocity for definitions and notations).
For an Eisenstein prime π, Nπ ≠ 3 and an Eisenstein integer α, gcd(α, π) = 1, define the quadratic character for Z[ω] by the formula
Let λ = a + b ω and μ = c + d ω be distinct Eisenstein primes where a and c are not divisible by 3 and b and d are divisible by 3. Eisenstein proved[29]
where 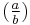 is the Jacobi symbol for Z.
is the Jacobi symbol for Z.
Imaginary quadratic fields
The laws in Z[i] and Z[ω] are special cases of more general laws that hold for the ring of integers in any imaginary quadratic number field.
Let k be an imaginary quadratic number field with ring of integers 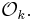 For a prime ideal
For a prime ideal 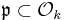 with odd norm
with odd norm 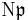 and
and 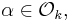 define the quadratic character for
define the quadratic character for 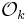 by the formula
by the formula
for an arbitrary ideal 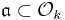 factored into prime ideals
factored into prime ideals 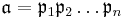 define
define
and for 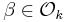 define
define
Let 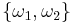 be an integral basis of
be an integral basis of 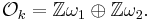
For 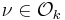 with odd norm Nν, define (ordinary) integers a, b, c, d by the equations,
with odd norm Nν, define (ordinary) integers a, b, c, d by the equations,
and define a function χ(ν) where ν has odd norm by
If m = Nμ and n = Nν are both odd, Herglotz proved[30]
Also, if 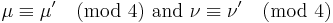 [31]
[31]
Polynomials over a finite field
Let F be a finite field with q = pn elements, where p is an odd prime number and n is positive, and let F[x] be the ring of polynomials in one variable with coefficients in F. If ![f,g \in \mathrm{F} [x]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/de3ed289c85629ff3214e178ee55c971.png) and f is irreducible, monic, and has positive degree, define the quadratic character
and f is irreducible, monic, and has positive degree, define the quadratic character 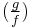 for F[x] in the usual manner:
for F[x] in the usual manner:
If 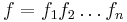 is a product of monic irreducibles let
is a product of monic irreducibles let
Dedekind[32] proved that if ![f,g \in \mathrm{F} [x]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/de3ed289c85629ff3214e178ee55c971.png) are monic and have positive degrees,
are monic and have positive degrees,
Higher powers
The attempt to generalize quadratic reciprocity for powers higher than the second was one of the main goals that led 19th century mathematicians, including Gauss, Dirichlet, Jacobi, Eisenstein, Dedekind, Kummer, and Hilbert to the study of general algebraic number fields and their rings of integers;[33] specifically Kummer invented ideals in order to state and prove higher reciprocity laws.
The ninth in the list of 23 unsolved problems which David Hilbert proposed to the Congress of Mathematicians in 1900 asked for the "Proof of the most general reciprocity law [f]or an arbitrary number field".[34] In 1923 Artin, building upon work by Furtwängler, Takagi, Hasse and others, discovered a general theorem for which all known reciprocity laws are special cases; he proved it in 1927.[35]
The links below provide more detailed discussions of these theorems.
See also
- Euler's criterion
- Zolotarev's lemma
- Proofs of quadratic reciprocity
- Cubic reciprocity
- Quartic reciprocity
- Artin reciprocity
Notes
- ↑ Gauss, DA § 4, arts 107–150
- ↑ E.g. in his mathematical diary entry for April 8, 1796 (the date he first proved quadratic reciprocity). See facsimile page from Felix Klein's Development of Mathematics in the 19th Century
- ↑ See F. Lemmermeyer's chronology and bibliography of proofs in the external references
- ↑ Lemmermeyer, pp. 2–3
- ↑ Gauss, DA, art. 182
- ↑ Lemmermeyer, p. 3
- ↑ Lemmermeyer, p. 5, Ireland & Rosen, pp. 54, 61
- ↑ Ireland & Rosen, pp. 69–70. His proof is based on what are now called Gauss sums.
- ↑ This section is based on Lemmermeyer, pp. 6–8
- ↑ The equivalence is Euler's criterion
- ↑ The analogue of Legendre's original definition is used for higher-power residue symbols
- ↑ E.g. Kronecker's proof (Lemmermeyer, ex. p. 31, 1.34) is to use Gauss's lemma to establish that
- ↑ Gauss, DA, arts 108–116
- ↑ Gauss, DA, arts 117–123
- ↑ Gauss, DA, arts 130
- ↑ Gauss, DA, Art 131
- ↑ Gauss, DA, arts. 125–129
- ↑ Gauss, DA, arts 135–144
- ↑ Because the basic Gauss sum equals
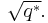
- ↑ Because the quadratic field
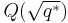 is a subfield of the cyclotomic field
is a subfield of the cyclotomic field 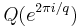
- ↑ Ireland & Rosen, pp 60–61.
- ↑ Gauss, "Summierung gewisser Reihen von besonderer Art", reprinted in Untersuchumgen uber hohere Arithmetik, pp.463–495
- ↑ Lemmermeyer, Th. 2.28, pp 63–65
- ↑ Lemmermeyer, ex. 1.9, p. 28
- ↑ By Dirichlet in 1837
- ↑ Gauss, BQ § 60
- ↑ Dirichlet's proof is in Lemmermeyer, Prop. 5.1 p.154, and Ireland & Rosen, ex. 26 p. 64
- ↑ Lemmermeyer, Prop. 5.1, p. 154
- ↑ Lemmermeyer, Thm. 7.10, p. 217
- ↑ Lemmermeyer, Thm 8.15, p.256 ff
- ↑ Lemmermeyer Thm. 8.18, p. 260
- ↑ Bach & Shallit, Thm. 6.7.1
- ↑ Lemmermeyer, p. 15, and Edwards, pp.79–80 both make strong cases that the study of higher reciprocity was much more important as a motivation than Fermat's Last Theorem was
- ↑ Lemmermeyer, p. viii
- ↑ Lemmermeyer, p. ix ff
References
The Disquisitiones Arithmeticae has been translated (from Latin) into English and German. The German edition includes all of Gauss's papers on number theory: all the proofs of quadratic reciprocity, the determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes. Footnotes referencing the Disquisitiones Arithmeticae are of the form "Gauss, DA, Art. n".
- Gauss, Carl Friedrich; Clarke, Arthur A. (translator into English) (1986), Disquisitiones Arithemeticae (Second, corrected edition), New York: Springer, ISBN 0-387-96254-9
- Gauss, Carl Friedrich; Maser, Hermann (translator into German) (1965), Untersuchungen über höhere Arithmetik (Disquisitiones Arithemeticae & other papers on number theory) (Second edition), New York: Chelsea, ISBN 0-8284-0191-8
The two monographs Gauss published on biquadratic reciprocity have consecutively-numbered sections: the first contains §§ 1–23 and the second §§ 24–76. Footnotes referencing these are of the form "Gauss, BQ, § n".
- Gauss, Carl Friedrich (1828), Theoria residuorum biquadraticorum, Commentatio prima, Göttingen: Comment. Soc. regiae sci, Göttingen 6
- Gauss, Carl Friedrich (1832), Theoria residuorum biquadraticorum, Commentatio secunda, Göttingen: Comment. Soc. regiae sci, Göttingen 7
These are in Gauss's Werke, Vol II, pp. 65–92 and 93–148. German translations are in pp. 511–533 and 534–586 of Untersuchungen über höhere Arithmetik.
Every textbook on elementary number theory (and quite a few on algebraic number theory) has a proof of quadratic reciprocity. Two are especially noteworthy:
Franz Lemmermeyer's Reciprocity Laws: From Euler to Eisenstein has many proofs (some in exercises) of both quadratic and higher-power reciprocity laws and a discussion of their history. Its immense bibliography includes literature citations for 196 different published proofs for the quadratic reciprocity law.
Kenneth Ireland and Michael Rosen's A Classical Introduction to Modern Number Theory also has many proofs of quadratic reciprocity (and many exercises), and covers the cubic and biquadratic cases as well. Exercise 13.26 (p 202) says it all
-
Count the number of proofs to the law of quadratic reciprocity given thus far in this book and devise another one.
- Bach, Eric; Shallit, Jeffrey (1966), Algorithmic Number Theory (Vol I: Efficient Algorithms), Cambridge: The MIT Press, ISBN 0-262-02045-5
- Edwards, Harold (1977), Fermat's Last Theorem, New York: Springer, ISBN 0-387-90230-9
- Lemmermeyer, Franz (2000), Reciprocity Laws: from Euler to Eisenstein, Berlin: Springer, ISBN 3-540-66967-4
- Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (second edition), New York: Springer, ISBN 0-387-97329-X
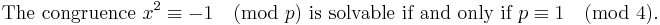
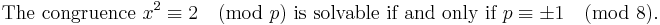
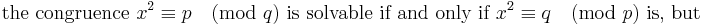
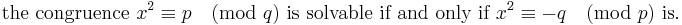
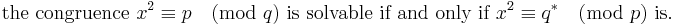
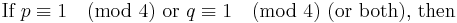
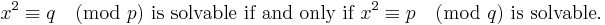
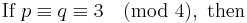
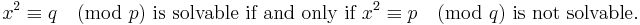
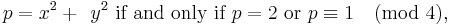
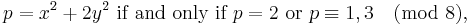
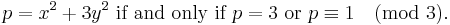
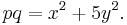
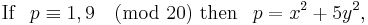
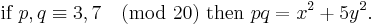
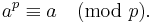
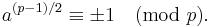
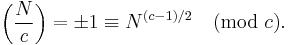
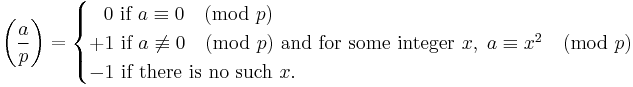
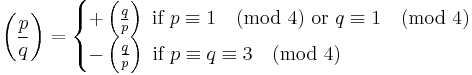
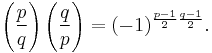
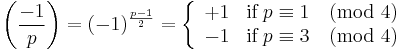
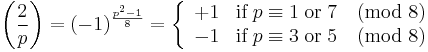
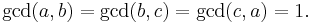
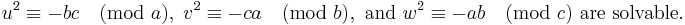
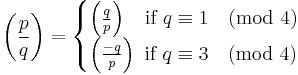
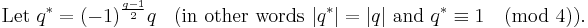
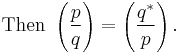
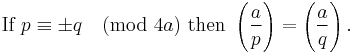
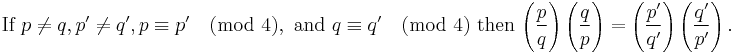
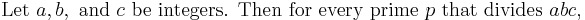
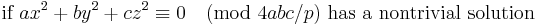
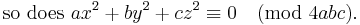
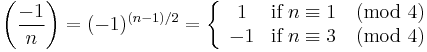
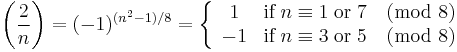
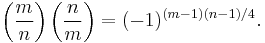
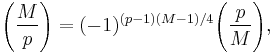
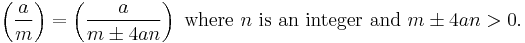
![\begin{align}
\left[\frac{\alpha}{\pi}\right]_2 &=
\pm 1 \equiv \alpha^\frac{\mathrm{N} \pi - 1}{2}\pmod{\pi} \\&=
\begin{cases}
+1 \mbox{ if }\gcd(\alpha, \pi) = 1 \mbox{ and there is a Gaussian integer }\eta \mbox{ such that } \alpha \equiv \eta^2 \pmod{\pi} \\
-1 \mbox{ if } \gcd(\alpha, \pi) = 1 \mbox{ and there is no such }\eta.
\end{cases}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/27d88f3ebe9932e2a9136797cdb8f8b5.png)
![\Bigg[\frac{\lambda}{\mu}\Bigg]_2 = \Bigg[\frac{\mu}{\lambda}\Bigg]_2, \;\;\;\;
\Bigg[\frac{i}{\lambda}\Bigg]_2 =(-1)^\frac{b}{2}, \;\; \mbox{ and }\;\;
\Bigg[\frac{1+i}{\lambda}\Bigg]_2 =\Bigg(\frac{2}{a+b}\Bigg),](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/37f39a92ed909f97feea1882f4afc96d.png)
![\begin{align}
\left[\frac{\alpha}{\pi}\right]_2 &=
\pm 1 \equiv \alpha^\frac{\mathrm{N} \pi - 1}{2}\pmod{\pi} \\&=
\begin{cases}
+1 \mbox{ if }\gcd(\alpha, \pi) = 1 \mbox{ and there is an Eisenstein integer }\eta \mbox{ such that } \alpha \equiv \eta^2 \pmod{\pi} \\
-1 \mbox{ if } \gcd(\alpha, \pi) = 1 \mbox{ and there is no such }\eta.
\end{cases}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d062f71a92e92a7f8a70c3532d4b52c3.png)
![\left[\frac{\lambda}{\mu}\right]_2 \bigg[\frac{\mu}{\lambda}\bigg]_2 =
(-1)^{\frac{\mathrm{N} \lambda - 1}{2}\frac{\mathrm{N} \mu-1}{2}},\;\;\;\;
\bigg[\frac{1-\omega}{\lambda}\bigg]_2 =\bigg(\frac{a}{3}\bigg), \;\; \mbox{ and }\;\;
\bigg[\frac{2}{\lambda}\bigg]_2 =\bigg(\frac{2}{\mathrm{N} \lambda }\bigg),](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/71657a8c072da5ba86ab93fe2adeca73.png)
![\begin{align}
\left[\frac{\alpha}{\mathfrak{p} }\right]_2 & \equiv \alpha^\frac{\mathrm{N} \mathfrak{p} - 1}{2}\pmod{\mathfrak{p} } \\&=
\begin{cases}
+1 \mbox{ if }\alpha\not\in \mathfrak{p} \mbox{ and there is an }\eta \in \mathcal{O}_k \mbox{ such that } \alpha - \eta^2 \in \mathfrak{p} \\
-1 \mbox{ if } \alpha\not\in \mathfrak{p} \mbox{ and there is no such }\eta \\
\;\;\;0 \mbox{ if } \alpha\in \mathfrak{p},
\end{cases}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/03cd3be189c0bc1dbad3889b6cae7e2e.png)
![\bigg[\frac{\alpha}{\mathfrak{a}}\bigg]_2 = \left[\frac{\alpha}{\mathfrak{p}_1 }\right]_2\left[\frac{\alpha}{\mathfrak{p}_2 }\right]_2 \dots \left[\frac{\alpha}{\mathfrak{p}_n }\right]_2,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/a76db03b874cf27efd10b6395ba06f58.png)
![\bigg[\frac{\alpha}{\beta}\bigg]_2 = \bigg[\frac{\alpha}{\beta \mathcal{O}_k}\bigg]_2.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/745acaa030121046e64714eff3faef50.png)
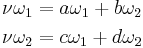
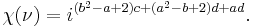
![\Bigg[\frac{\mu}{\nu}\Bigg]_2 \left[\frac{\nu}{\mu}\right]_2 =
(-1)^{\frac{m-1}{2}\frac{n-1}{2}}
\chi(\mu)^{m\frac{n-1}{2}}
\chi(\nu)^{-n\frac{m-1}{2}}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9dd4b438523a52a1d996dc51f41820ba.png)
![\Bigg[\frac{\mu}{\nu}\Bigg]_2 \left[\frac{\nu}{\mu}\right]_2 =
\Bigg[\frac{\mu'}{\nu'}\Bigg]_2 \left[\frac{\nu'}{\mu'}\right]_2.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/861443f1a198875716271b6a0f832574.png)
![\left(\frac{g}{f}\right) =
\begin{cases}
+1 \mbox{ if }\gcd(f,g)=1 \mbox{ and there are } h,k \in \mathrm{F} [x] \mbox{ such that }g-h^2 = kf \\
-1 \mbox{ if }\gcd(f,g)=1 \mbox{ and } g \mbox{ is not a square }\pmod{f}\\
\;\;\;0\mbox{ if }\gcd(f,g)\ne 1.
\end{cases}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c2c59ddc9108d3e70b0ee11584e7ecb2.png)